Binary Algorithms
I suspect these kinds of algorithms have already been better explained elsewhere, but if so I can’t seem to find where, so I might as well write this up.
Suppose you’re trying to find all possible permutations of a string: you have ABC, and you want to be able to derive ACB, BAC, etc. One simple way to do this is to think of the total number of permutations (equal to factorial(n)) as a binary number that contains a set of instructions on how to swap the elements of the string. 2*3*1 would of course be six, which in binary is 110. In this way, the binary numbers from 000 to 101 will be interpreted as instructions either to swap or not to swap the element at that position with the one previous to it. So, ABC with 000 will be the original string ABC – no letter is swapped. 001 will be ACB, with the third element swapped with the one before.
We can implement this in Python like so:
from math import factorial
def permute(s):
mutations = []
length = len(s)
chars = [c for c in s] # we must convert string to list for mutability
for x in range(factorial(length)):
sub_chars = chars[:]
for n in range(length):
if x>>n&1: # swap if bit at n is 1
sub_chars[n],sub_chars[n-1] = sub_chars[n-1], sub_chars[n]
mutations.append("".join(sub_chars))
return(mutations)
Notice the bitwise operators >> and & that allow us to shift and compare bits in a binary fashion.
This algorithm came to mind again while playing the Zachtronics game Exapunks (which essentially is a delightful assortment of tightly designed programming puzzles). Note that what follows is a spoiler for one of the puzzles! I would recommend saving it unless you have already seen it or have no desire to play the game!
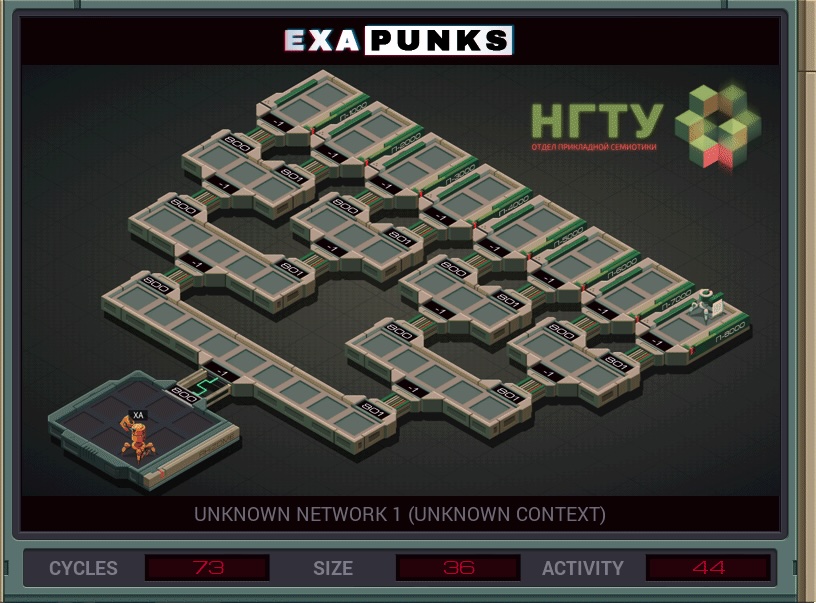
As you can see, you have a little programmable robot called an Exa that you need to guide to the destination file, which can exist at the end of any of the eight branches. There is no function to detect or otherwise direct the Exa to scan for the file or the other EXA who is holding it, so we need to find a way to keep generating Exas until we have explored every branch of the computer network.
EXAs are programmed using a simple language which is apparently similar to low-level languages like assembly code. Here we do not have the handy Python bitwise functions, but we need a similar algorithm to ensure we explore each branch. How shall we implement it?
Well, of course, the essence of translating any base ten number into binary is to divide it by two and check the remainder – a remainder will translate into a 1 bit, otherwise we will have 0. (This is actually more similar to how Heap’s Algorithm is implemented for generating permutations. ) Since we know there are eight possible permutations, we can simple count from 8 down to 1. So for 8, which represents perhaps the decision to take a right branch at each turn, we could do as follows:
COPY 7 X; Copy our value to the X register
MARK LOOP
MODI X 2 T; Check the value for X%2 and assign it to T (a kind of boolean register)
DIVI X 2 X; In Python, this would be X//=2
TJMP LEFT; If true, go left
LINK 800
TEST X > 0
TJMP LOOP
FJMP END
MARK LEFT
LINK 801
TEST X > 0
TJMP LOOP
MARK END
KILL
GRAB 275
LINK -1
LINK -1
LINK -1
DROP
This code is not too bad as a first draft, but it has a few issues and will not work. While as an algorithm it will get us the binary translation for any decimal digits, that is not exactly what we want. For one thing, we need to repeat this code to get the “binary” values for all digits from 0-7 to get all the combinations we want. Exapunks provides us a command REPLthat will do nicely, but we will need to take some care in its implementation. Secondly, the check of X > 0 as the termination condition of the loop will only work for some binary values – for example, it will obviously terminate too early when X = 0! We want to make sure it performs the operation exactly three times, or yields three ‘bits.’ One way we could do this would be to use the Tto count down, but we’re already using that register to store the value for the result of the modulo calculation.
The option I decided to go with was to initialize a file with three values, 0,0,0, to essentially act as an array to store the binary bits. Once we reach the end of the file, we know we’re done. This looks like:
MARK MAKEFILE
MAKE
COPY 0 F
COPY 0 F
COPY 0 F
SEEK -5; Rewind to beginning of file
MARK MAKEROUTE
MODI X 2 F
DIVI X 2 X
TEST EOF; Have we got to the end?
FJMP MAKEROUTE
Then we just read the bits from the file we’ve made to determine our route; the last step is just to use REPL within a master loop to count down from 7 to 0, each time creating a new EXA and going through the process of making a file and performing the necessary divisions. Here’s what the completed solution looks like:
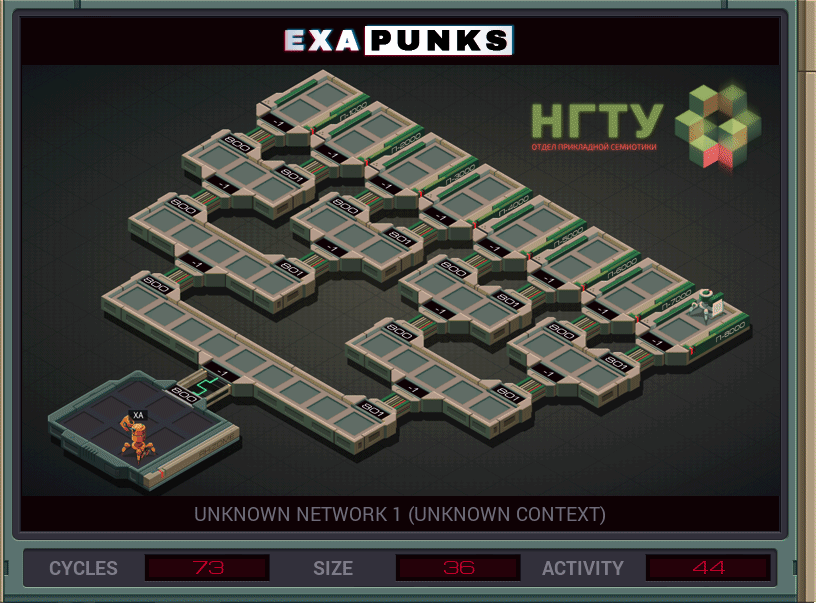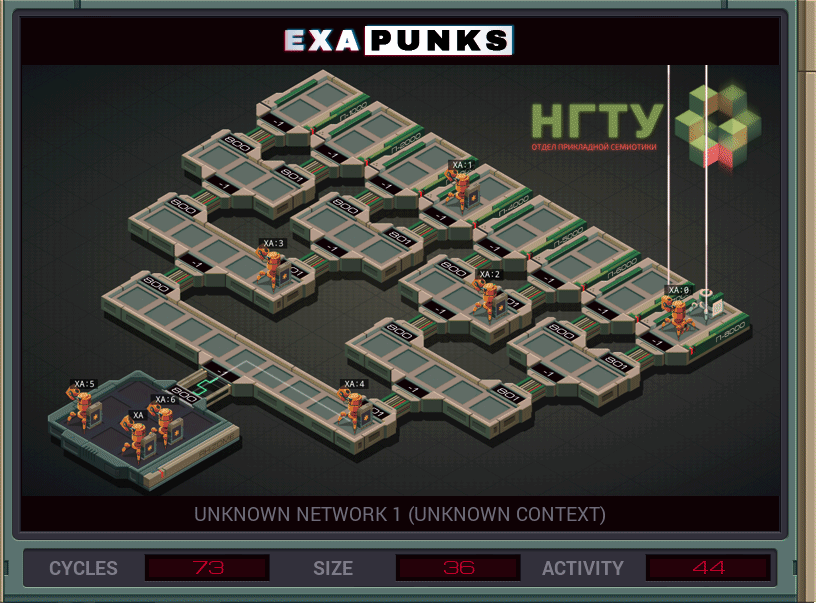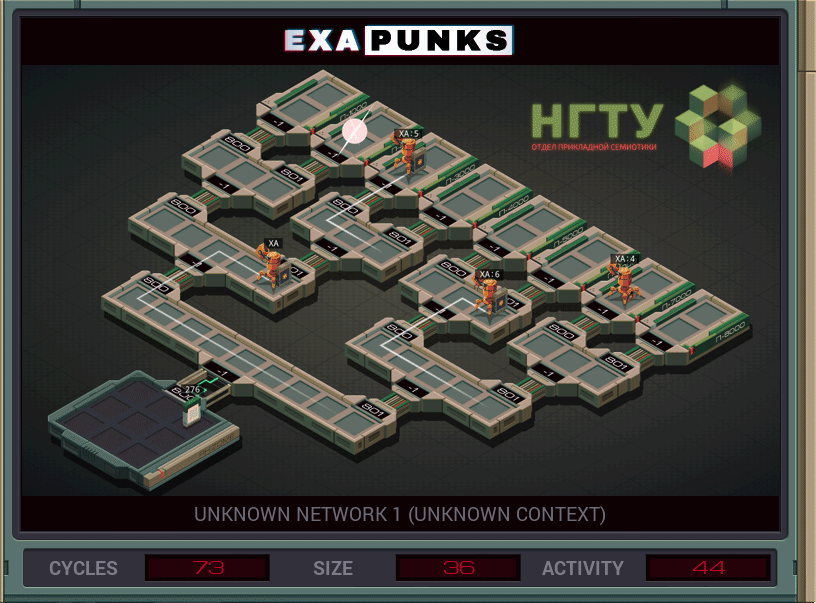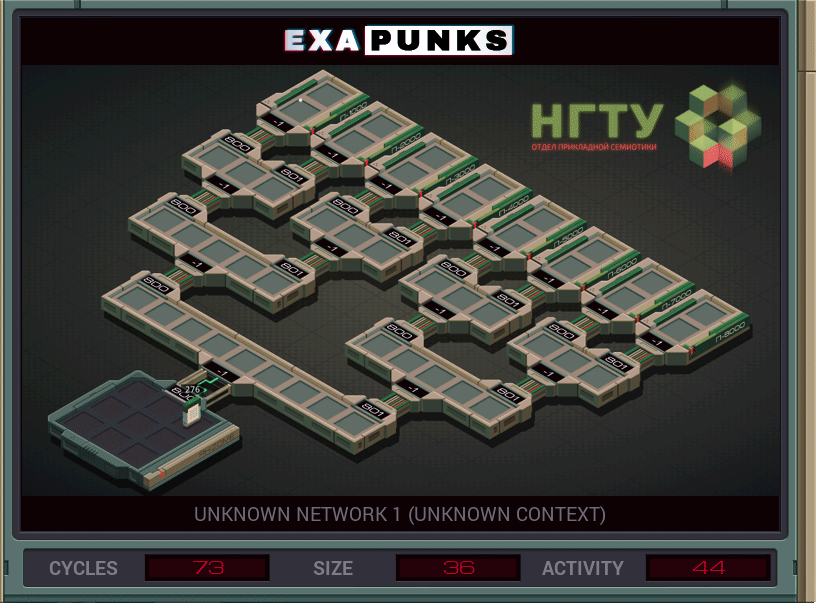
I am certain this is far from the most efficient solution, but what appeals to me about it is its conceptual simplicity and its use of the binary algorithm described above.